This week’s Riddler Express asks about a peculiar sequence of basketball games. Here’s the text of the puzzle, and my solution below.
Once a week, folks from Blacksburg, Greensboro, and Silver Spring get together for a game of pickup basketball. Every week, anywhere from one to five individuals will show up from each town, with each outcome equally likely.
Using all the players that show up, they want to create exactly two teams of equal size. Being a prideful bunch, everyone wears a jersey that matches the color mentioned in the name of their city. However, since it might create confusion to have one jersey playing for both sides, they agree that the residents of two towns will combine forces to play against the third town’s residents.
What is the probability that, on any given week, it’s possible to form two equal teams with everyone playing, where two towns are pitted against the third?
Extra credit: Suppose that, instead of anywhere from one to five individuals per town, anywhere from one to N individuals show up per town. Now what’s the probability that there will be two equal teams?
The probability of two teams of equal size in the 5-person case is $\frac{6}{25}$. More generally, the probability of forming two teams of equal size is $\frac{3n^2-3n}{2n^3}$.
To show how I arrived at this solution, begin by recognizing that the number of permutations with replacement represents the total number of possible teams that can be formed. The number of players is $N$ and the number of players teams is 3, so the denominator in our fraction of interest is $n^3$.
The numerator is a little trickier. In order to find its pattern, I wrote a function in R. I used the permutations package to generate all the possibilities of players that show up for each team for a given $N$. The total number of teams is ${3 \choose 2} = 3$: the Black and Green teams can join up to play against the Silver team, the Black and Silver teams can join up to play against the Green team, and the Green and Silver teams can join up to play against the Black team. Then, to determine whether or not a game is viable, we check whether or not the any of the combined teams are equal to a third team, e.g. if Black and Green have the same number of players as Silver, and so on. Here is the function and its output for $N = 2$.
library(arrangements)
library(dplyr)
basketball <- function(N) {
data <- as.data.frame(permutations(N, 3, replace = TRUE))
names(data) <- c("black", "green", "silver")
data <- data %>%
mutate(black_green = black + green,
black_silver = black + silver,
silver_green = silver + green,
game = ifelse(black_green == silver | black_silver == green | silver_green == black, TRUE, FALSE))
return(data)
}
| Black | Green | Silver | Black + Green | Black + Silver | Silver + Green | Game On? |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 2 | 2 | 2 | FALSE |
| 1 | 1 | 2 | 2 | 3 | 3 | TRUE |
| 1 | 2 | 1 | 3 | 2 | 3 | TRUE |
| 1 | 2 | 2 | 3 | 3 | 4 | FALSE |
| 2 | 1 | 1 | 3 | 3 | 2 | TRUE |
| 2 | 1 | 2 | 3 | 4 | 3 | FALSE |
| 2 | 2 | 1 | 4 | 3 | 3 | FALSE |
| 2 | 2 | 2 | 4 | 4 | 4 | FALSE |
If we apply this function for $N = 1, \dots, 10$ we can see a clear pattern emerge:
max_N <- 10
results <- lapply(1:max_N, basketball)
n <- 1:max_N
numerator <- sapply(1:max_N, function(n) sum(results[[n]]$game))
result_data_frame <- cbind.data.frame(n, numerator)
| N | Numerator |
|---|---|
| 1 | 0 |
| 2 | 3 |
| 3 | 9 |
| 4 | 18 |
| 5 | 30 |
| 6 | 45 |
| 7 | 63 |
| 8 | 84 |
| 9 | 108 |
| 10 | 135 |
The pattern is actually the same sequence as the triangular matchstick numbers—the number of matchsticks required to make an equilateral triangle out of matchsticks of $N$ “floors”—shifted by $N-1$. This is interesting given the connection between permutations and their geometric reprsentations. We can write the numerator as:
\[\frac{1}{2}3n^2 - 3n\]The probability is thus this numerator over the denominator we found earlier. Putting them together we arrive at our answer of $\frac{3n^2-3n}{2n^3}$.
It’s easy to see that the denominator grows more quickly than the numerator:
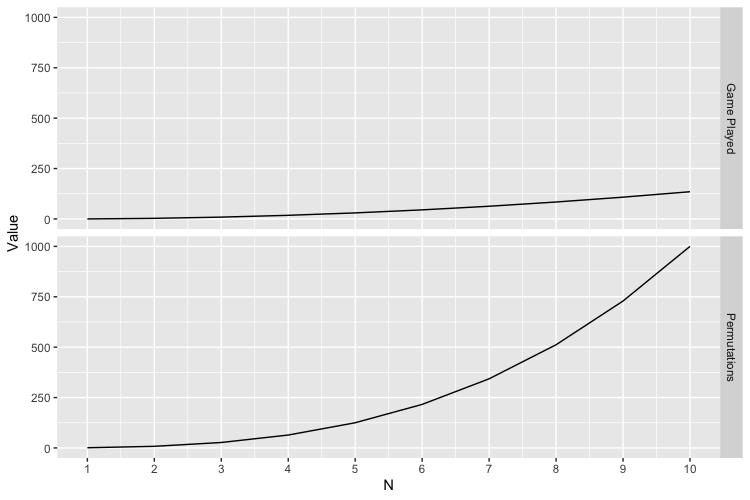
And that this number tends to zero as $N \to \infty$, which makes sense given that it would be hard to get equal-sized teams with the number of players from each of the three cities arriving somewhere in the narrow range between 1 and infinity. Of course, it’s also zero when $N = 1$.
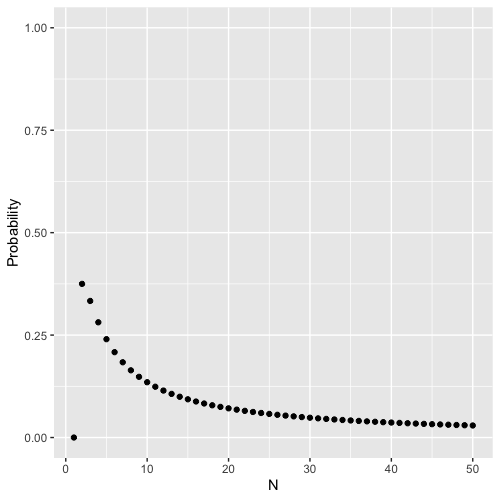
This was a fun problem! Big thanks to Sarah Wright for helping me think through its logic.
Here’s the code for the two figures:
library(ggplot2)
library(reshape2)
max_N <- 10
data <- tibble(1:max_N) %>%
rename(n = "1:max_N") %>%
mutate(numerator = (3*n^2 - 3*n)/2,
denominator = n^3,
answer = numerator/denominator)
melt(data, id.vars = "n") %>%
mutate(variable = case_when(
variable == "numerator" ~ "Game Played",
variable == "denominator" ~ "Permutations",
variable == "answer" ~ "Probability"
)) %>%
filter(variable != "Probability") %>%
rename(Value = "value",
N = "n",
Variable = "variable") %>%
ggplot(aes(x = N, y = Value)) + geom_line() +
facet_grid(Variable ~ .) +
scale_x_continuous(breaks = 0:10)
max_N <- 50
data <- tibble(1:max_N) %>%
rename(n = "1:max_N") %>%
mutate(numerator = (3*n^2 - 3*n)/2,
denominator = n^3,
answer = numerator/denominator)
data %>%
ggplot(aes(x = n, y = answer)) +
geom_point() + labs(x = "N", y = "Probability") +
scale_y_continuous(limits = 0:1)
And, just for fun, a Monte Carlo version. I wanted to practice avoiding a loop by using dplyr because I’ve been working on some permutation-related tasks for some of my own research on the detection of spillover effects—hopefully I can share some of that on this blog soon, as much as I love solving puzzles.
library(tidyr)
sims <- 10^6
max_N <- 5
data <- tibble(1:max_N) %>%
rename(n = "1:max_N") %>%
crossing(sim = 1:sims) %>%
group_by(sim, n) %>%
mutate(black = sample(1:n, 1),
green = sample(1:n, 1),
silver = sample(1:n, 1)) %>%
ungroup(n) %>%
mutate(game = ifelse(black + green == silver |
black + silver == green |
silver + green == black, TRUE, FALSE)) %>%
ungroup(sim)
results <- data %>%
group_by(n) %>%
summarise(mean = mean(game))